Iterative Tower of Hanoi

Tower of Hanoi is a mathematical puzzle. It consists of three poles and a number of disks of different sizes which can slide onto any poles. The puzzle starts with the disk in a neat stack in ascending order of size in one pole, the smallest at the top thus making a conical shape. The objective of the puzzle is to move all the disks from one pole (say ‘source pole’) to another pole (say ‘destination pole’) with the help of third pole (say auxiliary pole).

The puzzle has the following two rules:

      1. You can’t place a larger disk onto smaller disk
      2. Only one disk can be moved at a time

We have also seen that, for n disks, total 2n – 1 moves are required.

Iterative Algorithm:

1. Calculate the total number of moves required i.e. "pow(2, n)
   - 1" here n is number of disks.
2. If number of disks (i.e. n) is even then interchange destination 
   pole and auxiliary pole.
3. for i = 1 to total number of moves:
     if i%3 == 1:
 legal movement of top disk between source pole and 
        destination pole
     if i%3 == 2:
 legal movement top disk between source pole and 
        auxiliary pole 
     if i%3 == 0:
        legal movement top disk between auxiliary pole 
        and destination pole 

Example:

Let us understand with a simple example with 3 disks:
So, total number of moves required = 7

        S                      A                   D

When i= 1, (i % 3 == 1) legal movement between‘S’ and ‘D’ 



When i = 2,  (i % 3 == 2) legal movement between ‘S’ and ‘A’ 



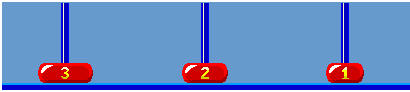When i = 3, (i % 3 == 0) legal movement between ‘A’ and ‘D’ ’



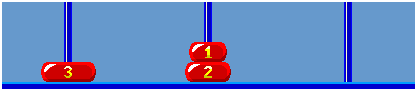When i = 4, (i % 4 == 1) legal movement between ‘S’ and ‘D’ 



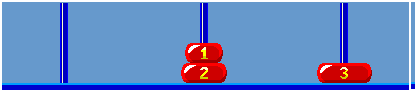When i = 5, (i % 5 == 2) legal movement between ‘S’ and ‘A’ 


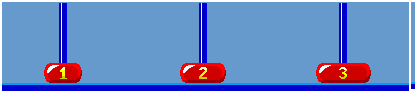When i = 6, (i % 6 == 0) legal movement between ‘A’ and ‘D’ 


When i = 7, (i % 7 == 1) legal movement between ‘S’ and ‘D’ 
 

So, after all these destination pole contains all the in order of size.
After observing above iterations, we can think thatafter a disk other than the smallest disk is moved, the next disk to be moved must be the smallest disk because it is the top disk resting on the spare pole and there are no other choices to move a disk.

// C Program for Iterative Tower of Hanoi

#include <stdio.h>

#include <math.h>

#include <stdlib.h>

#include <limits.h>

// A structure to represent a stack

struct Stack

{

   unsigned capacity;

   int top;

   int *array;

};

// function to create a stack of given capacity.

struct Stack* createStack(unsigned capacity)

{

    struct Stack* stack =

        (struct Stack*) malloc(sizeof(struct Stack));

    stack -> capacity = capacity;

    stack -> top = -1;

    stack -> array =

        (int*) malloc(stack -> capacity * sizeof(int));

    return stack;

}

// Stack is full when top is equal to the last index

int isFull(struct Stack* stack)

{

   return (stack->top == stack->capacity - 1);

}

// Stack is empty when top is equal to -1

int isEmpty(struct Stack* stack)

{

   return (stack->top == -1);

}

// Function to add an item to stack.  It increases

// top by 1

void push(struct Stack *stack, int item)

{

    if (isFull(stack))

        return;

    stack -> array[++stack -> top] = item;

}

// Function to remove an item from stack.  It

// decreases top by 1

int pop(struct Stack* stack)

{

    if (isEmpty(stack))

        return INT_MIN;

    return stack -> array[stack -> top--];

}

// Function to implement legal movement between

// two poles

void moveDisksBetweenTwoPoles(struct Stack *src,

            struct Stack *dest, char s, char d)

{

    int pole1TopDisk = pop(src);

    int pole2TopDisk = pop(dest);

    // When pole 1 is empty

    if (pole1TopDisk == INT_MIN)

    {

        push(src, pole2TopDisk);

        moveDisk(d, s, pole2TopDisk);

    }

    // When pole2 pole is empty

    else if (pole2TopDisk == INT_MIN)

    {

        push(dest, pole1TopDisk);

        moveDisk(s, d, pole1TopDisk);

    }

    // When top disk of pole1 > top disk of pole2

    else if (pole1TopDisk > pole2TopDisk)

    {

        push(src, pole1TopDisk);

        push(src, pole2TopDisk);

        moveDisk(d, s, pole2TopDisk);

    }

    // When top disk of pole1 < top disk of pole2

    else

    {

        push(dest, pole2TopDisk);

        push(dest, pole1TopDisk);

        moveDisk(s, d, pole1TopDisk);

    }

}

//Function to show the movement of disks

void moveDisk(char fromPeg, char toPeg, int disk)

{

    printf("Move the disk %d from \'%c\' to \'%c\'\n",

           disk, fromPeg, toPeg);

}

//Function to implement TOH puzzle

void tohIterative(int num_of_disks, struct Stack

             *src, struct Stack *aux,

             struct Stack *dest)

{

    int i, total_num_of_moves;

    char s = 'S', d = 'D', a = 'A';

    //If number of disks is even, then interchange

    //destination pole and auxiliary pole

    if (num_of_disks % 2 == 0)

    {

        char temp = d;

        d = a;

        a  = temp;

    }

    total_num_of_moves = pow(2, num_of_disks) - 1;

    //Larger disks will be pushed first

    for (i = num_of_disks; i >= 1; i--)

        push(src, i);

    for (i = 1; i <= total_num_of_moves; i++)

    {

        if (i % 3 == 1)

          moveDisksBetweenTwoPoles(src, dest, s, d);

        else if (i % 3 == 2)

          moveDisksBetweenTwoPoles(src, aux, s, a);

        else if (i % 3 == 0)

          moveDisksBetweenTwoPoles(aux, dest, a, d);

    }

}

// Driver Program

int main()

{

    // Input: number of disks

    unsigned num_of_disks = 3;

    struct Stack *src, *dest, *aux;

    // Create three stacks of size 'num_of_disks'

    // to hold the disks

    src = createStack(num_of_disks);

    aux = createStack(num_of_disks);

    dest = createStack(num_of_disks);

    tohIterative(num_of_disks, src, aux, dest);

    return 0;

}

Output:

Move the disk 1 from 'S' to 'D'
Move the disk 2 from 'S' to 'A'
Move the disk 1 from 'D' to 'A'
Move the disk 3 from 'S' to 'D'
Move the disk 1 from 'A' to 'S'
Move the disk 2 from 'A' to 'D'
Move the disk 1 from 'S' to 'D'