Circular Queue | (Introduction and Array Implementation)

Circular Queue

Circular queue avoids the wastage of space in a regular queue implementation using arrays.

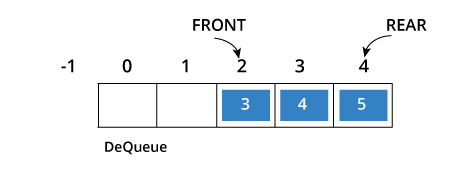
As you can see in the above image, after a bit of enqueueing and dequeueing, the size of the queue has been reduced.

The indexes 0 and 1 can only be used after the queue is reset when all the elements have been dequeued.

How Circular Queue Works

Circular Queue works by the process of circular increment i.e. when we try to increment any variable and we reach the end of queue, we start from the beginning of queue by modulo division with the queue size.

i.e.

if REAR + 1 == 5 (overflow!), REAR = (REAR + 1)%5 = 0 (start of queue)

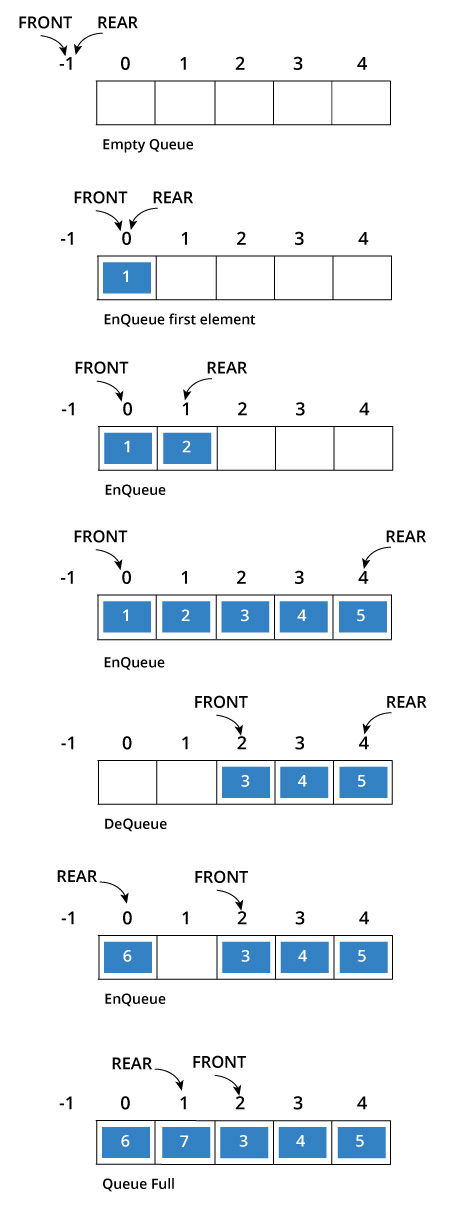
Queue operations work as follows:

• Two pointers called FRONT and REAR are used to keep track of the first and last elements in the queue.
• When initializing the queue, we set the value of FRONT and REAR to -1.
• On enqueing an element, we circularly increase the value of REAR index and place the new element in the position pointed to by REAR.
• On dequeueing an element, we return the value pointed to by FRONT and circularly increase the FRONT index.
• Before enqueing, we check if queue is already full.
• Before dequeuing, we check if queue is already empty.
• When enqueing the first element, we set the value of FRONT to 0.
• When dequeing the last element, we reset the values of FRONT and REAR to -1.

However, the check for full queue has a new additional case:

• Case 1: FRONT = 0 && REAR == SIZE - 1
• Case 2: FRONT = REAR + 1

The second case happens when REAR starts from 0 due to circular increment and when its value is just 1 less than FRONT, the queue is full.

Circular Queue Implementation in programming language

The most common queue implementation is using arrays, but it can also be implemented using lists.

When you run this program, the output will be

Inserted -> 1
  Inserted -> 2
  Inserted -> 3
  Inserted -> 4
  Inserted -> 5
  Queue is full!! 
 
  Front -> 0 
  Items -> 1 2 3 4 5 
  Rear -> 4 
 
  Deleted element -> 1 
 
  Front -> 1 
  Items -> 2 3 4 5 
  Rear -> 4 
 
  Inserted -> 7
  Front -> 1 
  Items -> 2 3 4 5 7 
  Rear -> 0 
 
  Queue is full!!