Optimal Substructure Property:-
In computer science, a problem is said to have optimal substructure if an optimal solution can be constructed efficiently from optimal solutions of its subproblems. This property is used to determine the usefulness of dynamic programming and greedy algorithms for a problem.
In simple term:-
Consider there is a problem (P1), with sub-problems (P2) within.
Let's call the solution to P1 as S1 and the solution to P2 as S2.
Now, you're able to design the best-possible solution for P2, and you've already done it, and that is S2.
If you're able to successfully design the solution for P1 using S2, then P1 is said to have an Optimal Substructure.
Real world example:-
the optimal way to make change for $1.99 (in terms of fewest coins used) is to use a 1 dollar coin and then find the optimal way to make change for the remaining $0.99. If you don’t make change for the remaining $0.99 optimally, the overall change for $1.99 won’t be optimal either.
Consider finding a shortest path for travelling between two cities by car, as illustrated in Figure 1. Such an example is likely to exhibit optimal substructure. That is, if the shortest route from A to D passes through B then C, then the shortest route from B to D must pass through C too. That is, the problem of how to get from B to D is nested inside the problem of how to get from A to D.
In computer science, a problem is said to have optimal substructure if an optimal solution can be constructed efficiently from optimal solutions of its subproblems. This property is used to determine the usefulness of dynamic programming and greedy algorithms for a problem.
In simple term:-
Consider there is a problem (P1), with sub-problems (P2) within.
Let's call the solution to P1 as S1 and the solution to P2 as S2.
Now, you're able to design the best-possible solution for P2, and you've already done it, and that is S2.
If you're able to successfully design the solution for P1 using S2, then P1 is said to have an Optimal Substructure.
Real world example:-
the optimal way to make change for $1.99 (in terms of fewest coins used) is to use a 1 dollar coin and then find the optimal way to make change for the remaining $0.99. If you don’t make change for the remaining $0.99 optimally, the overall change for $1.99 won’t be optimal either.
 |
| Figure 1 |
Consider finding a shortest path for travelling between two cities by car, as illustrated in Figure 1. Such an example is likely to exhibit optimal substructure. That is, if the shortest route from A to D passes through B then C, then the shortest route from B to D must pass through C too. That is, the problem of how to get from B to D is nested inside the problem of how to get from A to D.
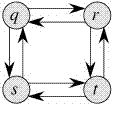
On the other hand, the Longest Path problem doesn’t have the Optimal Substructure property. Here by Longest Path we mean longest simple path (path without cycle) between two nodes. Consider the following unweighted graph given in the CLRS book. There are two longest paths from q to t: q→r→t and q→s→t. Unlike shortest paths, these longest paths do not have the optimal substructure property. For example, the longest path q→r→t is not a combination of longest path from q to r and longest path from r to t, because the longest path from q to r is q→s→t→r and the longest path from r to t is r→q→s→t.


No comments:
Post a Comment