Design a stack that supports getMin() in O(1) time and O(1) extra space

Question: Design a Data Structure SpecialStack that supports all the stack operations like push(), pop(), isEmpty(), isFull() and an additional operation getMin() which should return minimum element from the SpecialStack. All these operations of SpecialStack must be O(1). To implement SpecialStack, you should only use standard Stack data structure and no other data structure like arrays, list, .. etc.

Example:

Consider the following SpecialStack
16  --> TOP
15
29
19
18

When getMin() is called it should return 15, 
which is the minimum element in the current stack. 

If we do pop two times on stack, the stack becomes
29  --> TOP
19
18

When getMin() is called, it should return 18 
which is the minimum in the current stack.

In this article, a new approach is discussed that supports minimum with O(1) extra space. We define a variable minEle that stores the current minimum element in the stack. Now the interesting part is, how to handle the case when minimum element is removed. To handle this, we push “2x – minEle” into the stack instead of x so that previous minimum element can be retrieved using current minEle and its value stored in stack. Below are detailed steps and explanation of working.

Push(x) : Inserts x at the top of stack.

• If stack is empty, insert x into the stack and make minEle equal to x.
• If stack is not empty, compare x with minEle. Two cases arise:
  • If x is greater than or equal to minEle, simply insert x.
  • If x is less than minEle, insert (2*x – minEle) into the stack and make minEle equal to x. For example, let previous minEle was 3. Now we want to insert 2. We update minEle as 2 and insert 2*2 – 3 = 1 into the stack.

Pop() : Removes an element from top of stack.

• Remove element from top. Let the removed element be y. Two cases arise:
  • If y is greater than or equal to minEle, the minimum element in the stack is still minEle.
  • If y is less than minEle, the minimum element now becomes (2*minEle – y), so update (minEle = 2*minEle – y). This is where we retrieve previous minimum from current minimum and its value in stack. For example, let the element to be removed be 1 and minEle be 2. We remove 1 and update minEle as 2*2 – 1 = 3.

Important Points:

• Stack doesn’t hold actual value of an element if it is minimum so far.
• Actual minimum element is always stored in minEle

Illustration

Push(x)

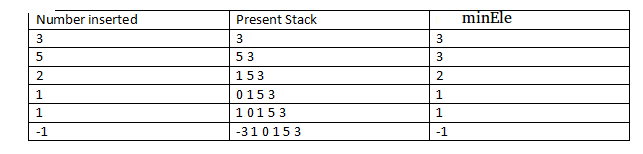
• Number to be Inserted: 3, Stack is empty, so insert 3 into stack and minEle = 3.
• Number to be Inserted: 5, Stack is not empty, 5> minEle, insert 5 into stack and minEle = 3.
• Number to be Inserted: 2, Stack is not empty, 2< minEle, insert (2*2-3 = 1) into stack and minEle = 2.
• Number to be Inserted: 1, Stack is not empty, 1< minEle, insert (2*1-2 = 0) into stack and minEle = 1.
• Number to be Inserted: 1, Stack is not empty, 1 = minEle, insert 1 into stack and minEle = 1.
• Number to be Inserted: -1, Stack is not empty, -1 < minEle, insert (2*-1 – 1 = -3) into stack and minEle = -1.

Pop()

• Initially the minimum element minEle in the stack is -1.
• Number removed: -3, Since -3 is less than the minimum element the original number being removed is minEle which is -1, and the new minEle = 2*-1 – (-3) = 1
• Number removed: 1, 1 == minEle, so number removed is 1 and minEle is still equal to 1.
• Number removed: 0, 0< minEle, original number is minEle which is 1 and new minEle = 2*1 – 0 = 2.
• Number removed: 1, 1< minEle, original number is minEle which is 2 and new minEle = 2*2 – 1 = 3.
• Number removed: 5, 5> minEle, original number is 5 and minEle is still 3

• C++

// C++ program to implement a stack that supports // getMinimum() in O(1) time and O(1) extra space. #include <bits/stdc++.h> using namespace std; // A user defined stack that supports getMin() in // addition to push() and pop() struct MyStack {     stack<int> s;     int minEle;     // Prints minimum element of MyStack     void getMin()     {         if (s.empty())             cout << "Stack is empty\n";         // variable minEle stores the minimum element         // in the stack.         else             cout <<"Minimum Element in the stack is: "                  << minEle << "\n";     }     // Prints top element of MyStack     void peek()     {         if (s.empty())         {             cout << "Stack is empty ";             return;         }         int t = s.top(); // Top element.         cout << "Top Most Element is: ";         // If t < minEle means minEle stores         // value of t.         (t < minEle)? cout << minEle: cout << t;     }     // Remove the top element from MyStack     void pop()     {         if (s.empty())         {             cout << "Stack is empty\n";             return;         }         cout << "Top Most Element Removed: ";         int t = s.top();         s.pop();         // Minimum will change as the minimum element         // of the stack is being removed.         if (t < minEle)         {             cout << minEle << "\n";             minEle = 2*minEle - t;         }         else             cout << t << "\n";     }     // Removes top element from MyStack     void push(int x)     {         // Insert new number into the stack         if (s.empty())         {             minEle = x;             s.push(x);             cout <<  "Number Inserted: " << x << "\n";             return;         }         // If new number is less than minEle         if (x < minEle)         {             s.push(2*x - minEle);             minEle = x;         }         else            s.push(x);         cout <<  "Number Inserted: " << x << "\n";     } }; // Driver Code int main() {     MyStack s;     s.push(3);     s.push(5);     s.getMin();     s.push(2);     s.push(1);     s.getMin();     s.pop();     s.getMin();     s.pop();     s.peek();     return 0; }

Output:

Number Inserted: 3
Number Inserted: 5
Minimum Element in the stack is: 3
Number Inserted: 2
Number Inserted: 1
Minimum Element in the stack is: 1
Top Most Element Removed: 1
Minimum Element in the stack is: 2
Top Most Element Removed: 2
Top Most Element is: 5

How does this approach work?
When element to be inserted is less than minEle, we insert “2x – minEle”. The important thing to notes is, 2x – minEle will always be less than x (proved below), i.e., new minEle and while popping out this element we will see that something unusual has happened as the popped element is less than the minEle. So we will be updating minEle.

How 2*x - minEle is less than x in push()? 
x < minEle which means x - minEle < 0

// Adding x on both sides
x - minEle + x < 0 + x 

2*x - minEle < x 

We can conclude 2*x - minEle < new minEle 

While popping out, if we find the element(y) less than the current minEle, we find the new minEle = 2*minEle – y.

How previous minimum element, prevMinEle is, 2*minEle - y
in pop() is y the popped element?

 // We pushed y as 2x - prevMinEle. Here 
 // prevMinEle is minEle before y was inserted
 y = 2*x - prevMinEle  

 // Value of minEle was made equal to x
 minEle = x .
 
 new minEle = 2 * minEle - y 
            = 2*x - (2*x - prevMinEle)
            = prevMinEle // This is what we wanted
 

Exercise:
Similar approach can be used to find the maximum element as well. Implement a stack that supports getMax() in O(1) time and constant extra space.